この記事では、「グラフ理論」を用いた問題解決に取り組む上で、知っておくべき概念を紹介していく。少し難解な内容も含まれるが、なるべく例も交えて解説をする。具体的に、この記事で紹介する概念は次の通りである。
| No | 用語(日本語) | 用語(英語) |
|---|---|---|
| 1 | グラフ理論 | graph theory |
| 2 | ノード | node |
| 3 | エッジ | edge |
| 4 | 完全グラフ | complete graph |
| 5 | 無向グラフ | undirected graph |
| 6 | 有向グラフ | directed graph |
| 7 | 循環グラフ | cyclic graph |
| 8 | 非循環グラフ | acyclic graph |
| 9 | 閉路 | cycle |
| 10 | 有向非循環グラフ | directed acyclic graph、DAG |
| 11 | オイラーグラフ | Eulerian graph |
| 12 | 半オイラーグラフ | semi-Eulerian graph |
| 13 | 次数 | degree |
| 14 | ハミルトングラフ | Hamilton graph |
| 15 | ディラックの定理 | Dirac’s theorem |
| 16 | オーレの定理 | Ore’s theorem |
| 17 | 連結グラフ | connected graph |
| 18 | 非連結グラフ | disconnected graph |
グラフ理論とは?
「グラフ理論(graph theory)」とは、ノードとエッジによって構成されたグラフを扱う数学の理論である。
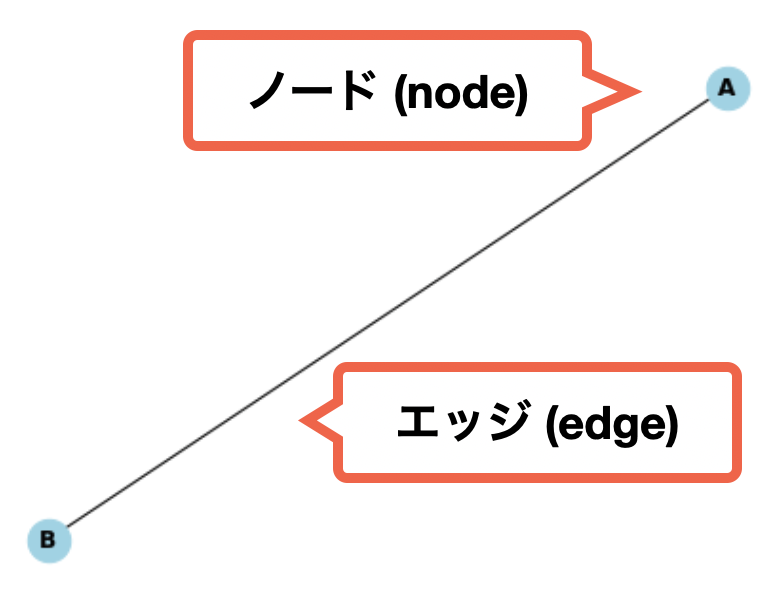
「ノード(node)」とは、グラフにおける頂点を指す。これは頂点(vertice)とも言う。「エッジ(edge)」とは、グラフにおける頂点と頂点を結ぶ線を指す。これはリンク(link)とも言う。
import networkx as nx
g = nx.Graph()
g.add_nodes_from(["A", "B"])
g.add_edges_from([("A", "B")])
nx.draw(g, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")グラフ理論は、現代においてビジネスや研究の分野で幅広く活用されている。以下に活用領域の例を示す。
- 脳神経ネットワーク
- ソーシャルネットワーク
- 交通網のネットワーク
- 感染症のネットワーク
- 口コミのネットワーク
グラフの種類
グラフ理論において登場するいくつかのグラフの種類の概念を紹介する。
完全グラフとは?
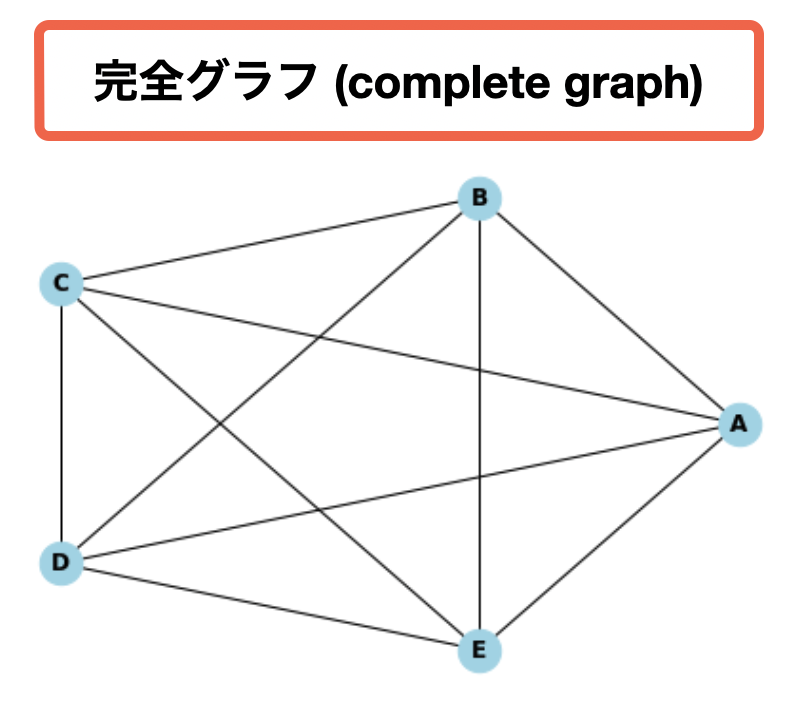
まず「完全グラフ(complete graph)」とは、全てのノード同士の間にエッジがあるグラフを指す。この時、ノードの数nに対して、エッジの数は(n(n-1)) / 2である。
import networkx as nx
import itertools
g = nx.Graph()
node_list = ["A", "B", "C", "D", "E"]
g.add_nodes_from(node_list)
edge_list = []
for pair in itertools.combinations(node_list, 2):
edge_list.append(pair)
g.add_edges_from(edge_list)
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")無向グラフ / 有向グラフとは?
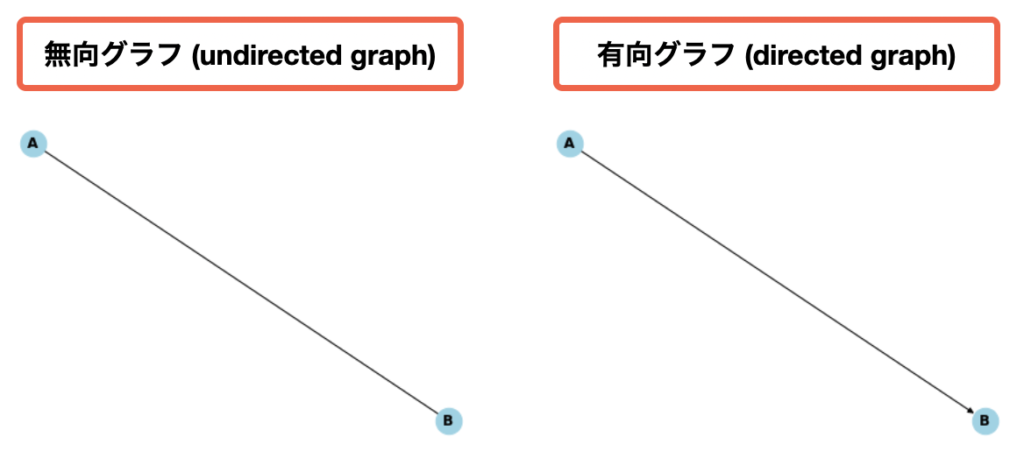
次に、「無向グラフ(undirected graph)」とは方向性のないエッジからなるグラフである。一方で、「有向グラフ(directed graph)」とは方向性のあるエッジからなるグラフである。
import networkx as nx
import matplotlib.pyplot as plt
# undirected graph
g = nx.Graph()
g.add_nodes_from(["A", "B"])
g.add_edges_from([("A", "B")])
nx.draw(g, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# directed graph
g_di = nx.DiGraph()
g_di.add_nodes_from(["A", "B"])
g_di.add_edges_from([("A", "B")])
nx.draw(g_di, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()循環グラフ / 非循環グラフとは?
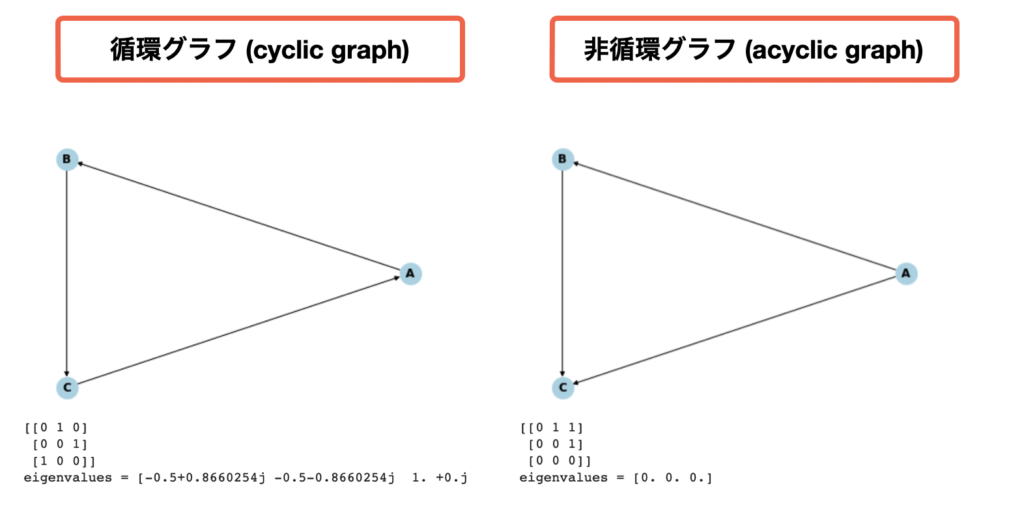
「循環グラフ(cyclic graph)」とは閉路のあるグラフである。「非循環グラフ(acyclic graph)」とは閉路のないグラフである。ここで、「閉路(cycle)」とは特定のノードから始まり、同じノードに戻る経路である。
また、非循環な有向グラフを「有向非循環グラフ(directed acyclic graph、DAG)」と言う。「非循環」のことを「非巡回」や「無閉路」と言う場合もある。
さらに、循環性の有無は、固有値を求めることで明らかにすることができる。閉路が存在しない時(非循環)は全ての固有値が0になる。
import networkx as nx
import matplotlib.pyplot as plt
import numpy.linalg as LA
# cyclic graph
g = nx.DiGraph()
node_list = ["A", "B", "C"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
z = nx.adjacency_matrix(g).todense()
w, v = LA.eig(z)
print(z)
print(f"eigenvalues = {w}")
# acyclic graph
g = nx.DiGraph()
node_list = ["A", "B", "C"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("A", "C")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
z = nx.adjacency_matrix(g).todense()
w, v = LA.eig(z)
print(z)
print(f"eigenvalues = {w}")オイラーグラフとは?
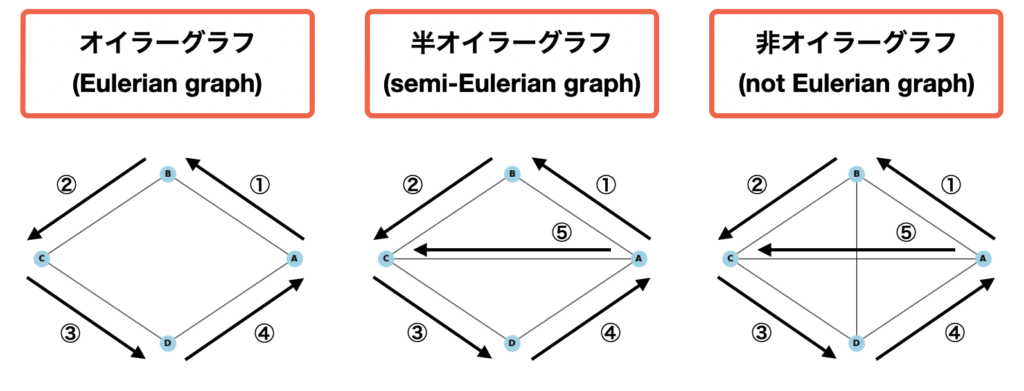
「オイラーグラフ(Eulerian graph)」とは、一筆書きをして戻ってくることができるグラフのことである。別の言い方をすると以下の条件を満たすグラフである。
- 全てのエッジを一度だけ通る。
- 始まりのノードに戻ってくる。
ちなみに、1番の条件(全てのエッジを一度だけ通る)を満たすが、2番の条件(始まりのノードに戻ってくる)を満たすことができないグラフを「半オイラーグラフ(semi-Eulerian graph)」と呼ぶ。
import networkx as nx
import matplotlib.pyplot as plt
# Eulerian graph
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# semi-Eulerian graph
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# not Eulerian graph
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C"), ("B", "D")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
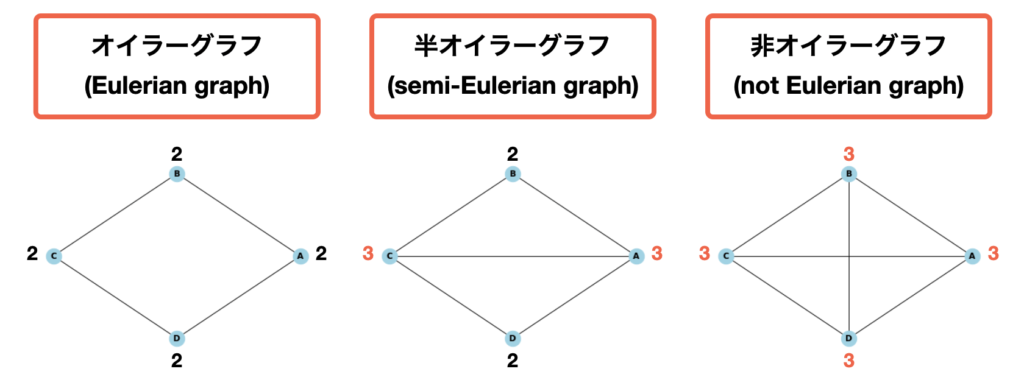
plt.show()ここで、全てのノードにおいて繋がっているエッジの数(「次数(degree)」)が偶数である時、オイラーグラフであると判定することができる。次数が奇数のノードが2つある時、半オイラーグラフと判定することができる。
ハミルトングラフとは?
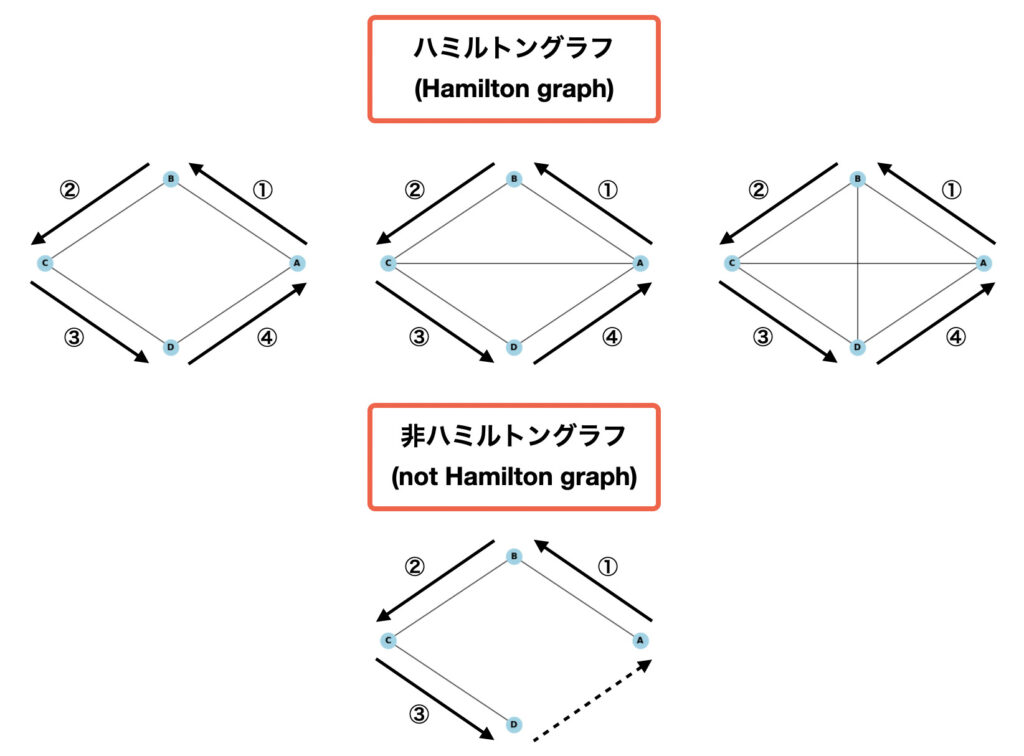
「ハミルトングラフ(Hamilton graph)」とは、全てのノードを一度だけ通って戻ることができるグラフである。
先程のオイラーグラフの例では、全てのグラフがハミルトングラフになる。
import networkx as nx
import matplotlib.pyplot as plt
# Hamilton graph (1)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# Hamilton graph (2)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# Hamilton graph (3)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C"), ("B", "D")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# not Hamilton graph
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()ここで、ハミルトングラフであることを判定する方法は二つある。ここで注意すべき点として、この二つを満たしていないからといって、ハミルトングラフではないことを証明できるわけではない。
ディラックの定理とは?
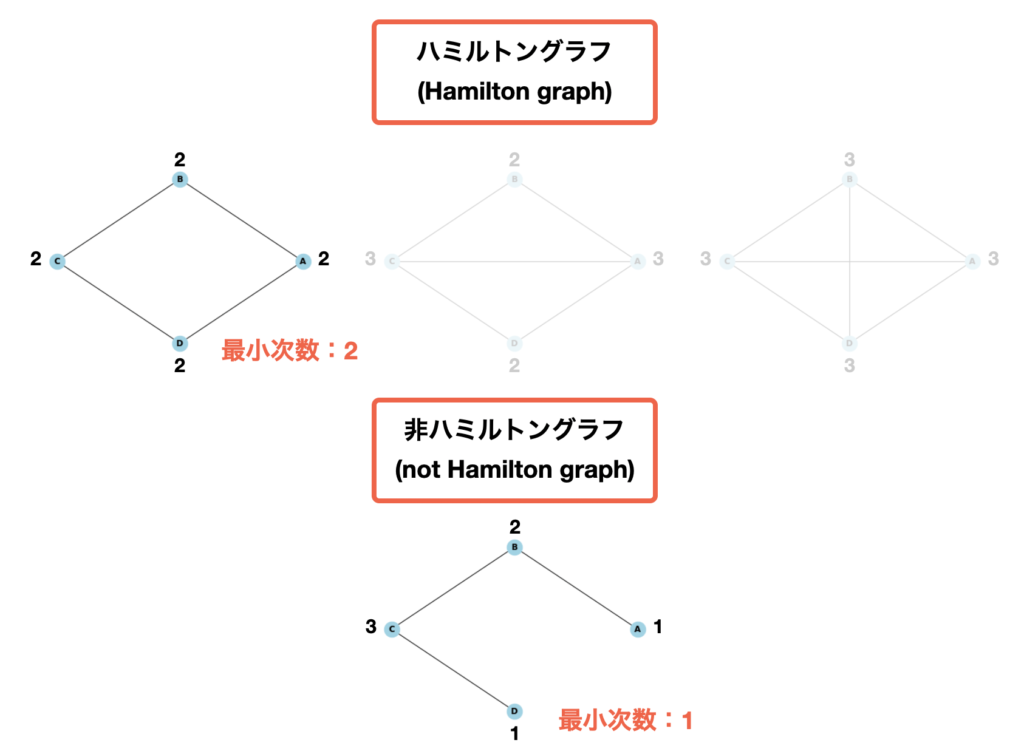
まず、「ディラックの定理(Dirac’s theorem)」では、全てのノードにおける次数dが、ノード数nの半分(n/2)以上の時、ハミルトングラフである。
先述した例において、左上のグラフにおいては、最小次数が2であり、ノード数は4であるため、2 ≧ (4 / 2)の不等式が成り立つため、ハミルトングラフであると言える。一方で、下のグラフにおいては、最小次数が1であり、ノード数は4であるため、1 ≧ (4 / 2)の不等式が成り立たないため、ハミルトングラフであると証明することはできない。
オーレの定理とは?
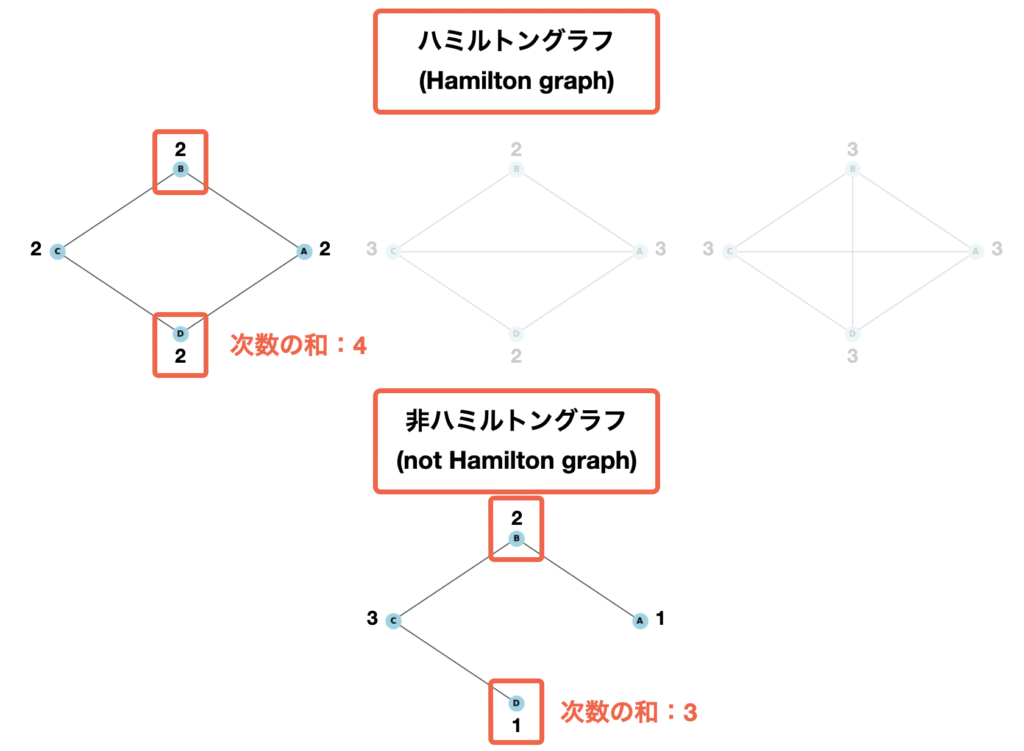
まず、「オーレの定理(Ore’s theorem)」では、隣接していないノード間の次数の合計が、ノード数n以上の時、ハミルトングラフである。
先述した例において、左上のグラフにおいては、隣接していないBとDの次数の合計は4であり、ノード数は4であるため、2 + 2 ≧ 4の不等式が成り立つため、ハミルトングラフであると言える。一方で、下のグラフにおいては、隣接していないBとDの次数の合計は3であり、ノード数は4であるため、2 + 1 ≧ 4の不等式が成り立たないため、ハミルトングラフであると証明することはできない。
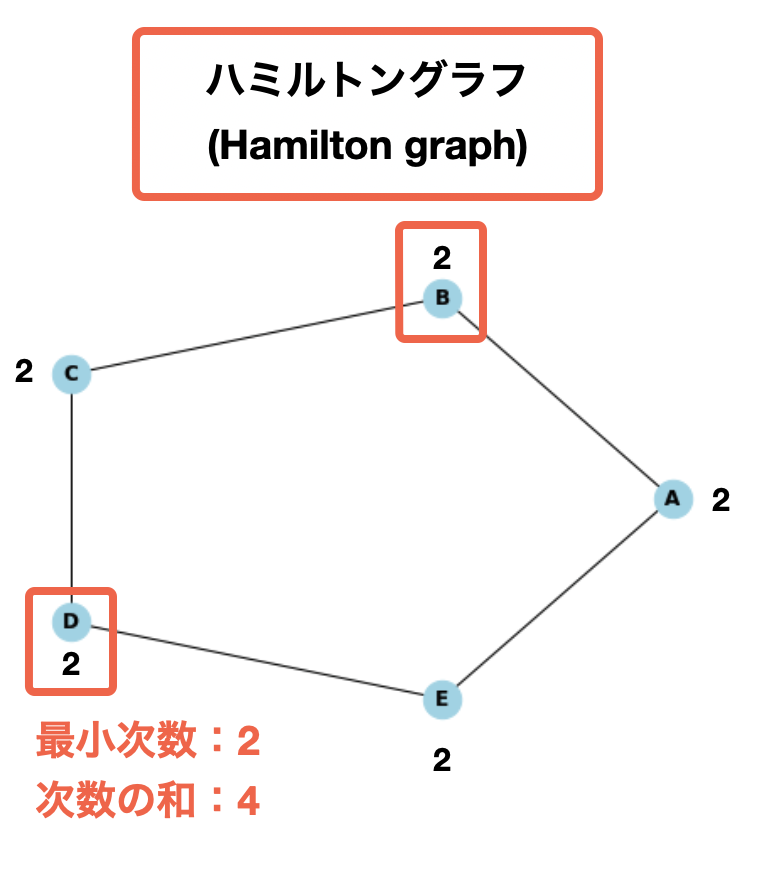
ここまでの説明を聞くと、ハミルトングラフを見つけるのは簡単だと思うかもしれない。では、次の例ではどうだろうか?
import networkx as nx
# Hamilton graph
g = nx.Graph()
node_list = ["A", "B", "C", "D", "E"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "E"), ("E", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")上記の例では、全てのノードを一度だけ通って戻ることができるため、ハミルトングラフであることは自明である。しかし、このグラフは、「ディラックの定理」にも「オーレの定理」にも当てはまらない。
最小次数は2であるが、ノード数は5であるため、2 ≧ 5 / 2は成り立たない(ディラックの定理)。
隣接していないBとDの次数の和は4であるが、ノード数は5であるため、2 + 2 ≧ 5は成り立たない(オーレの定理)。
このように、どちらの定理も間違ってはいないが、ハミルトングラフではないことを証明することは難しい。
連結グラフ / 非連結グラフとは?
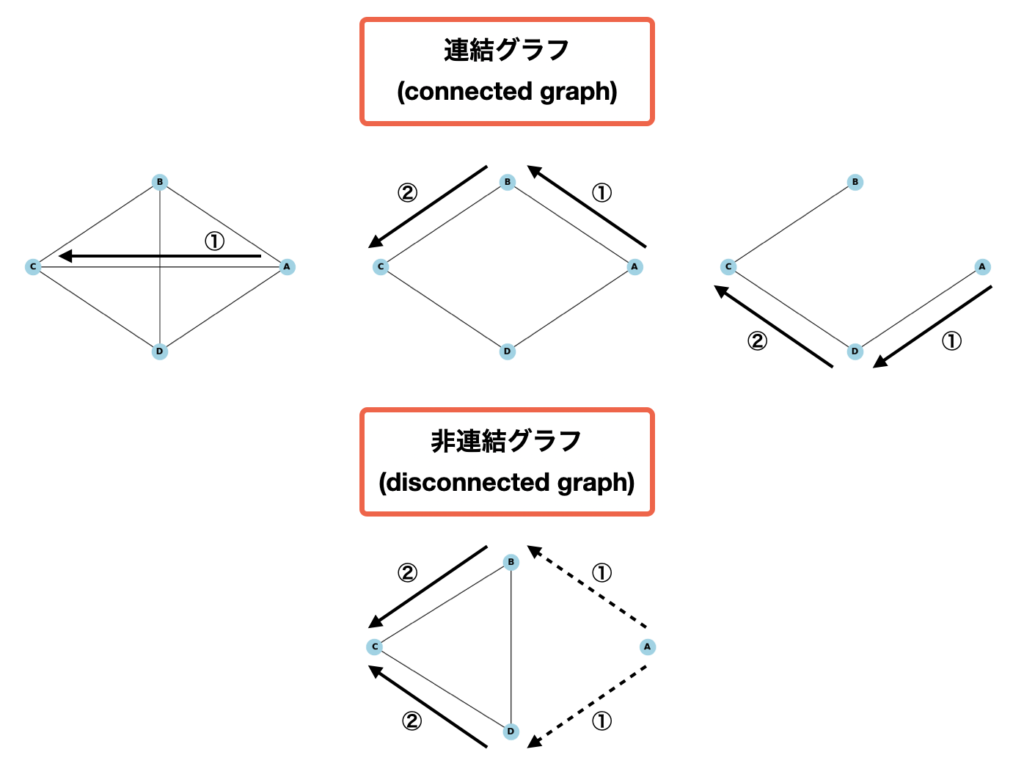
「連結グラフ(connected graph)」とは、全ての2ノード間において経路(道)が存在するグラフである。逆に、経路が存在しない2ノードの組み合わせが存在するグラフを「非連結グラフ(disconnected graph)」と言う。
ここで言う経路とは、直接的な経路でなくても、別のノードを中継した経路でも良い。
AからCのノードへの経路を考えた時の例は次の通りである。
import networkx as nx
import matplotlib.pyplot as plt
# connected graph (1)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C"), ("B", "D")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# connected graph (2)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# connected graph (3)
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("B", "C"), ("C", "D"), ("D", "A")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()
# disconnected graph
g = nx.Graph()
node_list = ["A", "B", "C", "D"]
g.add_nodes_from(node_list)
g.add_edges_from([("B", "C"), ("C", "D"), ("D", "B")])
pos = nx.circular_layout(g)
nx.draw(g, pos, node_size=500, node_color="lightblue", with_labels=True, font_weight="bold")
plt.show()最後に
いかがだったでしょうか?
この記事を通して、少しでもあなたの困りごとが解決したら嬉しいです^^
📩 仕事の相談はこちら 📩
お仕事の相談のある方は、下記のフォームよりお気軽にご相談ください。
問い合わせフォームはこちら
もしもメールでの問い合わせの方がよろしければ、下記のメールアドレスへご連絡ください。
info*galirage.com(*を@に変えてご送付ください)
🎁 「生成AIの社内ガイドライン」PDFを『公式LINE』で配布中 🎁
「LINEで相談したい方」や「お問い合わせを検討中の方」は、公式LINEでご連絡いただけますと幸いです。
(期間限定で配信中なため、ご興味ある方は、今のうちに受け取りいただけたらと思います^^)
公式LINEはこちら
🚀 新サービス開始のお知らせ 🚀
新サービス 「AI Newsletter for Biz」 がスタートしました!
ビジネスパーソン向けに「AIニュース」を定期配信する完全無料のニュースレターです📩
ますみが代表を務める「株式会社Galirage」では、「生成AIを用いたシステムの受託開発(アドバイス活動含む)」をしています。
そこでお世話になっているお客様に対して、「最新トレンドを加味したベストな提案」をするために、日々最新ニュースを収集する仕組みを構築していました。
今回は、そこで構築した仕組みを活用して、より多くの人に有益な情報を届けたいと思い、本サービスを開始しました!
一人でも多くの方にとって、「AI人材としてのスキルアップ」につながれば幸いです^^
▼ 登録はこちらから ▼
https://bit.ly/ai_newsletter_for_biz_ai_lab

参考文献
- 数理モデル入門(Ezaki, 2020)
- Pythonで学ぶネットワーク分析(Murata, 2019)
- グラフ理論(Shimokawa, 2018)
- グラフ理論入門 – DevelopersIO
- うさぎでもわかる離散数学