Kaggleにある「Credit Card Fraud Detection」というデータセットをPythonで簡単に分析,詐欺予測を行いました.
1. データセットの分析
1-a. データセット
このデータセットはcreditcard.csvだけで構成されており,サイズも143.84MBとデータセットの中では比較的小さめです.2日間で起こった284,807件の取引のうち492件の詐欺が記録されています(めっちゃデータ偏ってる!).直接的な入力データは示さず,PCA変換したデータ28次元で示しています.これに加え,データ収集時からの秒数,取引の量(多分ユーロ?)で特徴が表現されていて,出力となるクラスでは”1″が不正取引,”0″が正常な取引を示しています.実際に,CSVをPandasを用いて,Dataframeという形式で,読み込みます.Timeが0~172792のように秒ごとに記録されています.確かに2日分の取引情報が記録されていることがわかります.
import pandas as pd
transactions = pd.read_csv("creditcard.csv")
print(transactions)
#Output
# Time V1 V2 ... V28 Amount Class
#0 0.0 -1.359807 -0.072781 ... -0.021053 149.62 0
#1 0.0 1.191857 0.266151 ... 0.014724 2.69 0
#2 1.0 -1.358354 -1.340163 ... -0.059752 378.66 0
#3 1.0 -0.966272 -0.185226 ... 0.061458 123.50 0
#4 2.0 -1.158233 0.877737 ... 0.215153 69.99 0
#... ... ... ... ... ... ... ...
#284802 172786.0 -11.881118 10.071785 ... 0.823731 0.77 0
#284803 172787.0 -0.732789 -0.055080 ... -0.053527 24.79 0
#284804 172788.0 1.919565 -0.301254 ... -0.026561 67.88 0
#284805 172788.0 -0.240440 0.530483 ... 0.104533 10.00 0
#284806 172792.0 -0.533413 -0.189733 ... 0.013649 217.00 0
#
#[284807 rows x 31 columns]1-b. 特徴量とクラスの関係
各特徴量上の正・不正の分布を描画して各特徴量の関係とクラスの関係をSeabornという可視化ツールを使って見ていきたい.出力結果pairplot.pngでは,縦横軸,特徴量が並んでおり,縦軸は上から,横軸は左から,V1,V2・・・のように配置されています.各特徴量の交差しているところに対応している特徴同士の分布をプロットしています.青色が正常な取引で,オレンジ色が不正な取引を示しています.対角線上の分布は各特徴量の1変数のプロットを示しています.不正のクラスは正常なクラスに比べ,分布がまとまっていますが,多くの特徴次元では,正常な分布に内包されているか,重なっています.V3, V4, V9, V10, V11, V12, V14, V16, V17, V18は分布のズレを視覚的に確認できます.また,’amount’, V28, V23, V21, V20では分布が集中していることがわかります.これらの違いを多次元的に見るだけでもある程度の識別はできると考えられます.
import matplotlib.pyplot as plt
import seaborn as sns
sns.pairplot(transactions.iloc[:,1:],hue = "Class",diag_kind="kde")
plt.savefig('pairplot.png')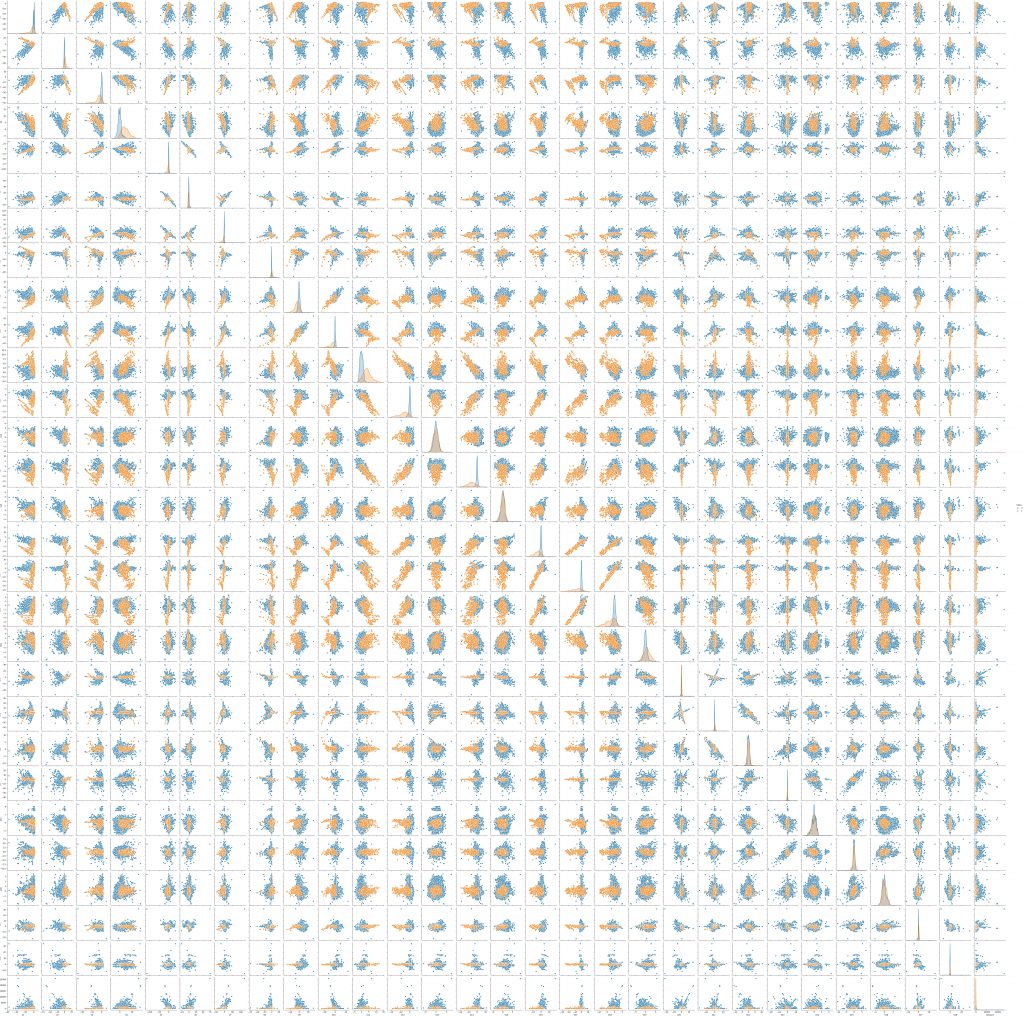
1-c. 特徴量の時間変化の関係
1-bでは時間方向は独立として図示して,分析しました.次に,書く特徴を独立として扱うと正・不正がどのように分布するかをみてみます.まず,不正直前の取引がどのようになっているのかをプロットしてみます.不正を100プロット目として,それ以前の特徴量を描画しました.左上から,順に右下まで各特徴量の時間プロットを示しています.しかし,どの特徴量においても定性的に時系列方向に特徴を確認することができませんでした.まあ,取引した記録といえど,同じ人がしたとは限らないので,時系列的に特徴があるとは考えにくいですね.
import numpy as np
fraud = transactions[transactions["Class"] == 1]
before = 100
wave = np.zeros([fraud.shape[0], fraud.shape[1], before+1])
for i in range(fraud.shape[0]):
wave[i,:,:] = transactions.iloc[fraud.index[i]-before:fraud.index[i]+1,:].T
for j in range(fraud.shape[1]):
df = pd.DataFrame(wave[:,j,:])
plt.figure()
plt.plot(df.T)
plt.savefig('df_V'+str(j)+'.png')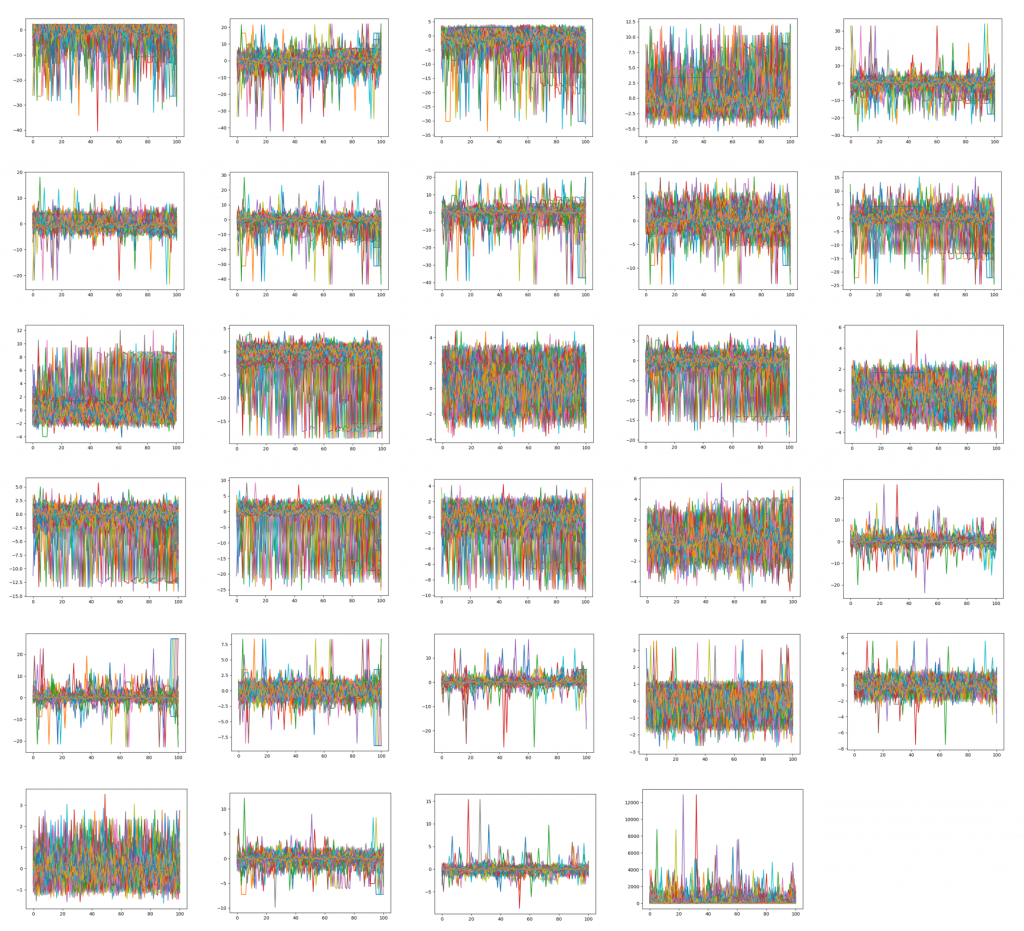
2. 詐欺の識別
では,実際に機械学習による詐欺の識別を行っていきます.
ロジスティック回帰
1.の様子から見るに,時系列の機械学習よりは一つの取引をそれぞれ独立と扱う方が,いい気がするので,典型的なロジスティック回帰で分類を図ってみたいと思います.
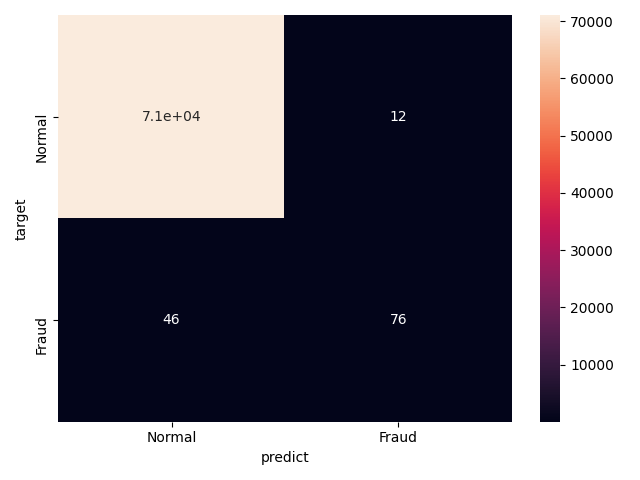
各特徴量を正規化したのち,ランダムにデータを4つに分け,クロスバリデーションで学習しました.この識別器の性能を見るために,accuracy, precision, recall, f値, 係数,混合行列を出力しました.係数と混合行列はそれぞれボックスプロットとヒートマップを用いて表現しました.係数マップは横軸=特徴量,縦軸=係数で示しており,絶対値が高ければ,それだけその変数が識別に寄与していることが言えます.混同行列のヒートマップは,左上と右下の値が高く,左下と右上の値が小さいほど,良い識別器であることが言えます.
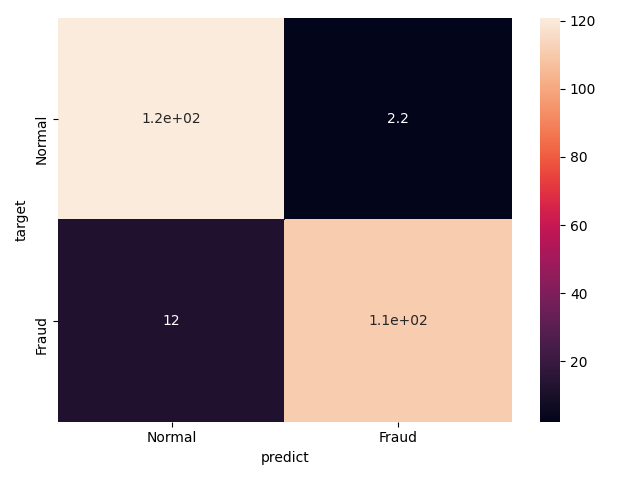
Resultsでは,accuracyは非常に高い値を示しいるのですが,precision, recall, f-scoreがそれに比べると低い値を示しています.また,混合行列のヒートマップでは,左上の値が非常に高いことがわかる.つまり,この結果は,正常と判断しやすい識別器になってしまっていることがこれらの結果から見えてきます.係数の図を見ると,実際に分類に寄与したのは,V4, V10, V14が大きいところであることが見えます.上記したPairplotと比較しても相違ないことが確認できます.
accuracy = 0.9991819022411386
precision = 0.8687427926932224
recall = 0.6219512195121951
f-score = 0.722974390199201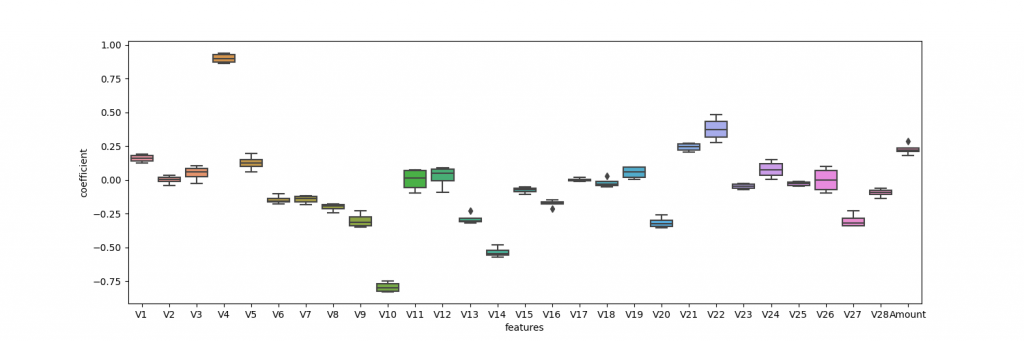
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler
target = transactions.iloc[:,30] #クラスだけを抽出
ss = StandardScaler()
transactions.loc[:,:] = ss.fit_transform(transactions) #正規化
data = transactions.iloc[:,1:30] #特徴量だけを抽出
kf = StratifiedKFold(n_splits = 4, shuffle = True) #クロスバリデーションの宣言
#結果を格納しておく空の変数を用意
coefs = np.zeros([4, 29])
intes = np.zeros([4, 1])
accuracy = np.zeros([4, 1])
precision = np.zeros([4, 1])
recall = np.zeros([4, 1])
fscore = np.zeros([4, 1])
confMs = np.zeros([4, 2, 2])
j = 0
for train, test in kf.split(data,target):
lr = LogisticRegression() #ロジスティック回帰を宣言
lr.fit(data.iloc[train], target.iloc[train]) #学習
answer = target.iloc[test]
predict = lr.predict(data.iloc[test])
accuracy[j,:] = accuracy_score(answer, predict) #accuracyの算出
precision[j,:] = precision_score(answer, predict) #precisionの算出
recall[j,:] = recall_score(answer, predict) #recallの算出
fscore[j,:] = f1_score(answer, predict) #F値の算出
coefs[j,:] = lr.coef_ #係数を抽出
intes[j,:] = lr.intercept_ #切片を抽出
confMs[j,:,:] = confusion_matrix(answer, predict) #混合行列の算出
j += 1
coefs_df = pd.DataFrame(coefs, columns=data.columns)
print(coefs_df)
print(intes)
print("accuracy = " + str(np.mean(accuracy)))
print("precision = " + str(np.mean(precision)))
print("recall = " + str(np.mean(recall)))
print("f-score = " + str(np.mean(fscore)))
plt.figure(figsize=(15,5))
sns.boxplot(x="features", y="coefficient", data=pd.melt(coefs_df, var_name="features", value_name="coefficient")) #係数をプロット
plt.savefig('coefficient.png')
confM = np.mean(confMs, axis = 0)
print(confM.shape)
plt.figure()
xtics=["Normal", "Fraud"]
ytics=["Normal", "Fraud"]
sns.heatmap(confM,xticklabels=xtics,yticklabels=ytics, annot=True) #混合行列をプロット
plt.xlabel("predict")
plt.ylabel("target")
plt.tight_layout()
plt.savefig('cofusionMatrix.png')この結果から,気に識別器は良いものではないことが見えるので,データセットの扱いを変える.両クラスが同じ割合になるように,正常な取引をランダムで間引いて,ロジスティック回帰を行い,同じ結果を算出してみる.間引きのコードを上記のプログラムの上流に加えます.以下に,各特徴量に対する係数,混合行列の図,precision,recall,f値を示します.これらの値が大幅に改善していることがわかります.
df = transactions.sort_values('Class')
normal = df.iloc[:284807-492,:].sample(n=492)
fraud = df.iloc[284807-492:,:]
trans = pd.concat([normal, fraud], axis=0).sample(frac=1)
accuracy = 0.9420731707317074
precision = 0.9801689643602236
recall = 0.9024390243902439
f-score = 0.9395426498152178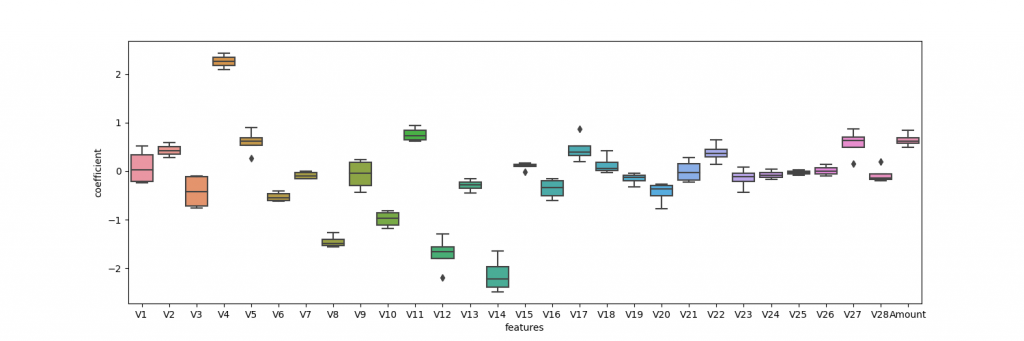
RandomForest
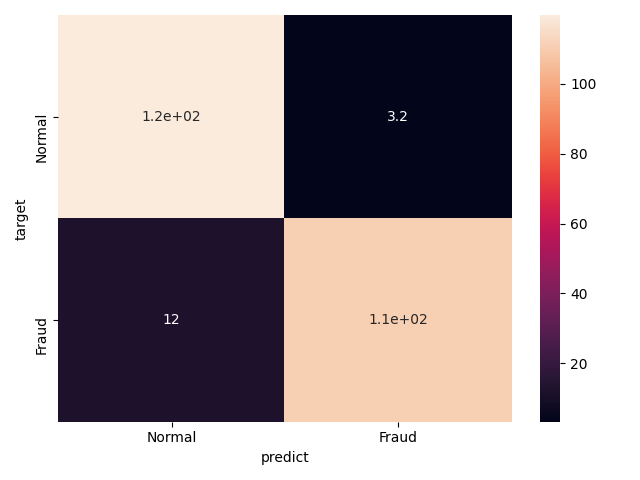
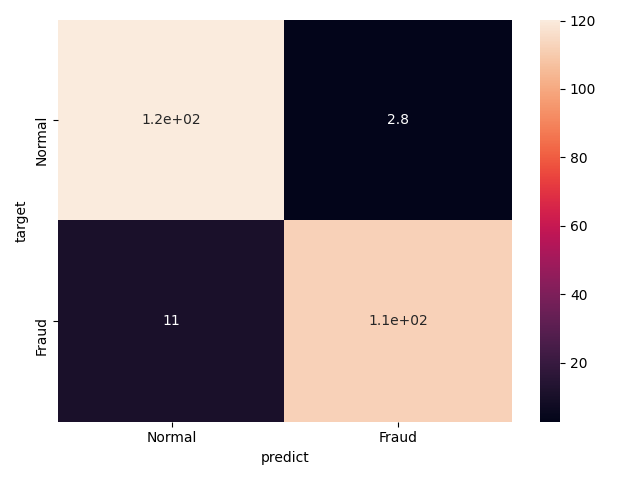
別のモデルでよく使われるモデルの1つであるRandomForestを試してみる.本来なら,パラメータチューニングを行うが,本記事は厳密なコンペではないため,割愛させていただきます.ロジスティック回帰と同様な前処理を施し,クロスバリデーション,評価の算出も同様です.プログラムはクロスバリデーション内のみ示します.結果をみると,ロジスティック回帰の結果とほぼ同様な結果であることが確認できます.
accuracy = 0.9380081300813008
precision = 0.9715614267673764
recall = 0.9024390243902439
f-score = 0.9356403994574136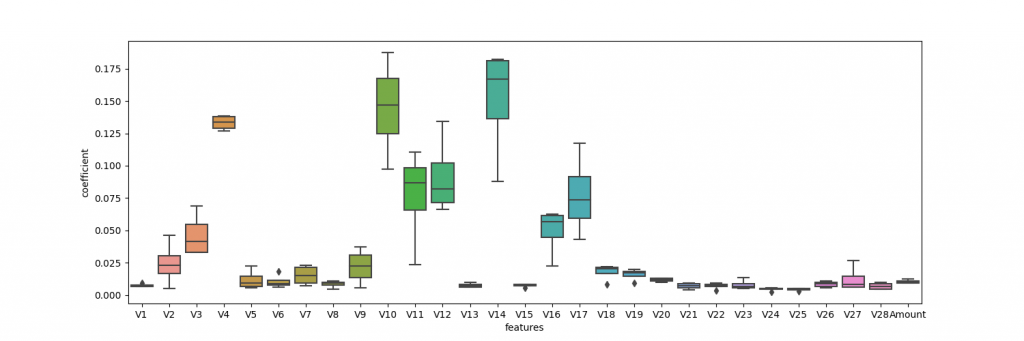
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(max_depth=30, n_estimators=30)
rf.fit(data.iloc[train], target.iloc[train])
answer = target.iloc[test]
predict = rf.predict(data.iloc[test])
accuracy[j,:] = accuracy_score(answer, predict)
precision[j,:] = precision_score(answer, predict)
recall[j,:] = recall_score(answer, predict)
fscore[j,:] = f1_score(answer, predict)
coefs[j,:] = rf.feature_importances_
confMs[j,:,:] = confusion_matrix(answer, predict)
j += 1XGBoost
次に,XGBoostというアルゴリズムを試してみる.これも同様な前処理,解析方法で結果を算出しました.これも,ロジスティック回帰,RandomForestとほとんど変わらない.
accuracy = 0.9451219512195121
precision = 0.9762810544671484
recall = 0.9126016260162602
f-score = 0.9430332779180052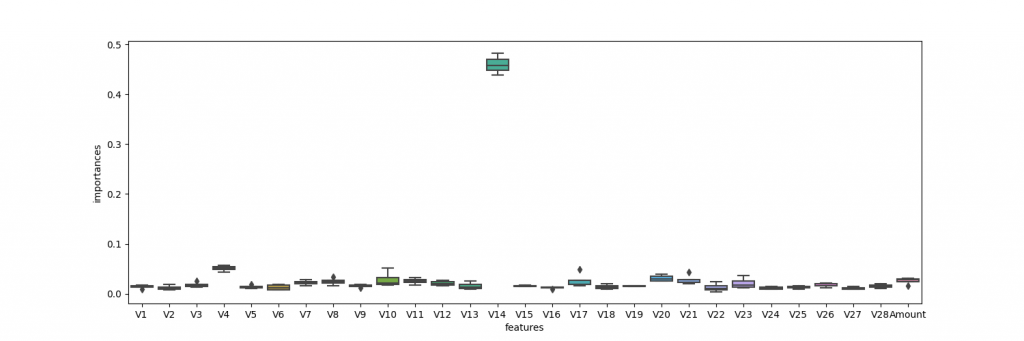
import xgboost as xgb
xg = xgb.XGBClassifier(objective='binary:logistic',
max_depth = 5,
learning_rate=0.1,
n_estimators=100)
xg.fit(data.iloc[train], target.iloc[train])
answer = target.iloc[test]
predict = xg.predict(data.iloc[test])
accuracy[j,:] = accuracy_score(answer, predict)
precision[j,:] = precision_score(answer, predict)
recall[j,:] = recall_score(answer, predict)
fscore[j,:] = f1_score(answer, predict)
coefs[j,:] = xg.feature_importances_
confMs[j,:,:] = confusion_matrix(answer, predict)
j += 1SVM
最後にSVMを試してみる.これも同様な前処理,解析方法で結果を算出しました.この結果は,precisionに結果が偏っていることがわかります.
accuracy = 0.8983739837398375
precision = 0.9948118279569893
recall = 0.8008130081300813
f-score = 0.8870274099648281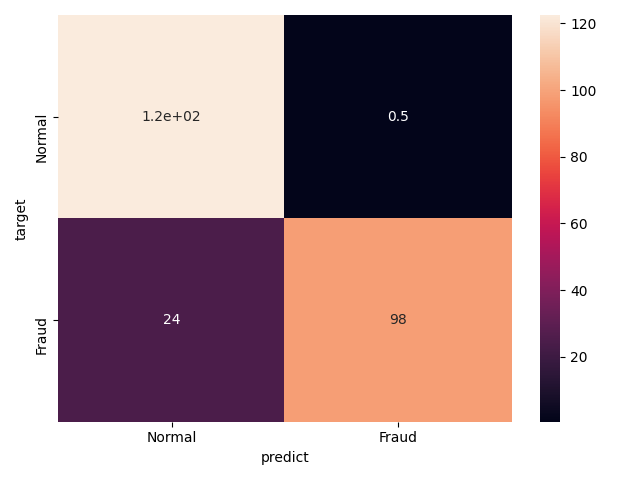
from sklearn.svm import SVC
sv = SVC(gamma=0.001)
sv.fit(data.iloc[train], target.iloc[train])
answer = target.iloc[test]
predict = sv.predict(data.iloc[test])
accuracy[j,:] = accuracy_score(answer, predict)
precision[j,:] = precision_score(answer, predict)
recall[j,:] = recall_score(answer, predict)
fscore[j,:] = f1_score(answer, predict)
confMs[j,:,:] = confusion_matrix(answer, predict)
j += 1まとめ
これまで,簡単な分析とロジスティック回帰,RandomForest,XGBoost,SVMを扱ってきました.このまとめとして,データ整形が分類精度に強く寄与していたことがわかります.このほかにもニューラルネットやエラスチック回帰などなど,様々な機械学習アルゴリズムやアンサンブル学習することで,もっと精度上げることができると考えられます.
最後まで読んでいただきありがとうございます!