この記事は、Kerasと言われるライブラリを初めて触る人向けの超入門記事として執筆しました。機械学習(Machine Learning; ML)を用いて予想をしますが、正式な検証や評価よりも簡易的に走り切れる仕様になっています。
1. Kerasとは?
まずKerasの公式サイトでは、以下のように解説されています。
Kerasは,Pythonで書かれた,TensorFlowまたはCNTK,Theano上で実行可能な高水準のニューラルネットワークライブラリです. Kerasは,迅速な実験を可能にすることに重点を置いて開発されました. アイデアから結果に到達するまでのリードタイムをできるだけ小さくすることが,良い研究をするための鍵になります.
簡単に言うと、「ニューラルネットワークをとても簡単に実装することができるライブラリ」ということですね。ちなみに、TensorFlowは、Kerasの骨格とも言えるライブラリになります。
TensorFlow を利用すると、パソコン、モバイル、ウェブ、およびクラウドで使える機械学習モデルを、エキスパートはもちろん初心者でも簡単に作成できます。まずは以下の各セクションをご覧ください。
2. KerasとTensorflowのインストール
まだPythonの環境構築ができていない方は、こちらの記事を参考にして準備しましょう。
【macOSの方々】
【Windowsの方々】
参考 Pythonの開発環境を用意しよう!(Windows)Progate – プログラミングで人生の可能性を広げよう
それでは、pipを用いて、kerasというライブラリ(パッケージ)をインストールしていきましょう。
Package Installer for Pythonのこと。
Pythonのパッケージ管理を行うためのコマンド。
terminalやコマンドプロンプトを開き、以下のようにコマンドを実行します。
$ pip install keras tensorflow以上のようにインストールをしていないと、以下のようなエラーが出てくると思います。また、pythonのv3.7以降だとエラーが出る事例が報告されているため、3.6系にするとうまくいくことがあります。
ModuleNotFoundError: No module named 'keras'
ModuleNotFoundError: No module named 'tensorflow'3. sin波を予測してみよう!
3-a. sin波の生成
まずは、教師データとなるsin波を生成していきましょう。教師データとは、答えがわかっているデータのことで、これを使って機械に学習させていきます。
以下のようにnumpyとmatplotlibを用いて、生成と表示をしてみましょう。
import numpy as np
import matplotlib.pyplot as plt
# === 3-a. データの作成 ===
x = np.linspace(-np.pi, np.pi).reshape(-1, 1)
t = np.sin(x)
plt.plot(x, t)
plt.show()すると、以下のようにsin波が描出できるのが確認できます。
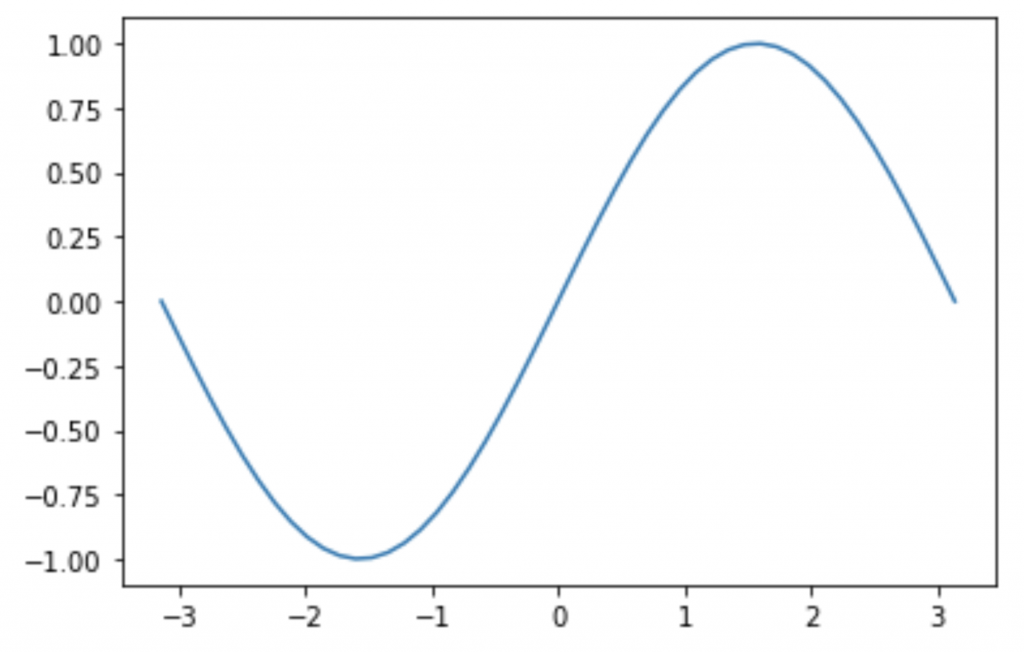
3-b. モデルの生成
続いて、sin波を予測するためのモデルを作成していきます。
今回は、ハイパーパラメータ(バッチサイズ、ニューロン数、層数、活性化関数など)については決めうちしていますが、詳しくはまた別の記事でまとめたいと思います。
from keras.models import Sequential
from keras.layers import Dense
# === 3-b. モデルの作成 ===
# パラメータを設定
batch_size = 8 # バッチサイズ
n_in = 1 # 入力層のニューロン数
n_mid = 20 # 中間層のニューロン数
n_out = 1 # 出力層のニューロン数
# ニューラルネットワークのモデルを生成
model = Sequential()
model.add(Dense(n_mid, input_shape=(n_in,), activation="sigmoid"))
model.add(Dense(n_out, activation="linear"))
model.compile(loss="mean_squared_error", optimizer="sgd")
print(model.summary())すると、出力は以下のように出てくると思います。
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 20) 40
_________________________________________________________________
dense_2 (Dense) (None, 1) 21
=================================================================
Total params: 61
Trainable params: 61
Non-trainable params: 0
_________________________________________________________________
None入力層(Input: 1)=> 中間層(Middle: 20) => 出力層(Output: 1)というような3層のモデルになっていることを表します。
(余談ですが、入力層をカウントせず2層と言う場合もあります。)
パラメーターについては、重み係数(weight)とバイアス項(bias term)があるため、中間層は40個(20weight + 20bias)、出力層は21個(20weight + 1bias)になっています。
3-c. モデルの学習
これで準備は整ったので、モデルに学習させてみましょう。
historyには、学習推移が保存されます。学習には数分かかると思います。
また、ここではvalidation_splitを0.1にしているため、10%を検証データに、90%を訓練データに使用しています。
# === 3-c. モデルの学習 ===
history = model.fit(x, t, batch_size=batch_size, epochs=2000, validation_split=0.1)3-d. 学習推移の可視化
historyを可視化することで、学習がうまくいっているかを確認しましょう。
今回は、一度しか訓練データと検証データを分割していないため、簡略化した方法であるHold-out法を用いています。本来は、Cross Validation(k-分割交差検証)などを使う方が妥当ですが、それについては以下の記事を参考にしてみてください。
参考 学習データとテストデータの分割手法についてAI人工知能テクノロジー
それでは、訓練データと検証データのloss(誤差)を可視化してみましょう。
# === 3-d. 学習推移の可視化 ===
loss_train = history.history['loss']
loss_val = history.history['val_loss']
plt.plot(np.arange(len(loss_train)), loss_train, label="loss_train")
plt.plot(np.arange(len(loss_val)), loss_val, label="loss_val")
plt.legend()
plt.show()訓練データ(blue)が学習するのは当然ですが、検証データ(orange)もしっかりと学習していることがわかりますね。
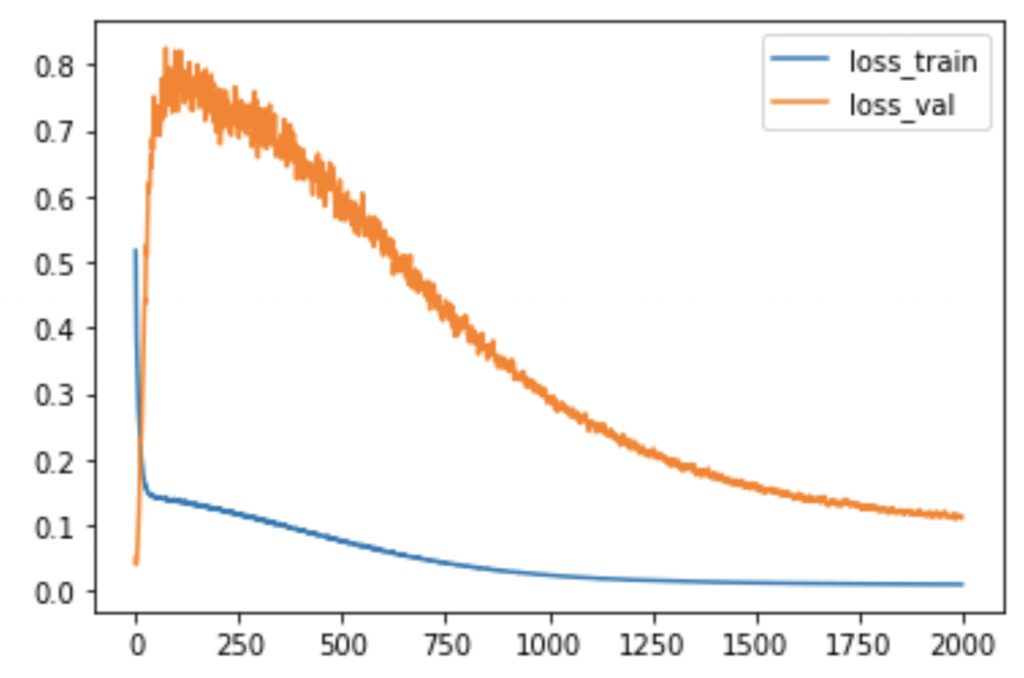
3-e. sin波の予測
最後に、学習させたモデルを用いて予測してみましょう。本来は、教師データと異なるデータで予測できるかを試さなくてはいけませんが、簡易的に同じ区間のデータで予測をしましょう。
# === 3-e. sin波の予測 ===
plt.plot(x, model.predict(x))
plt.plot(x, t)
plt.show()定性的に予測ができていることが確認できました。
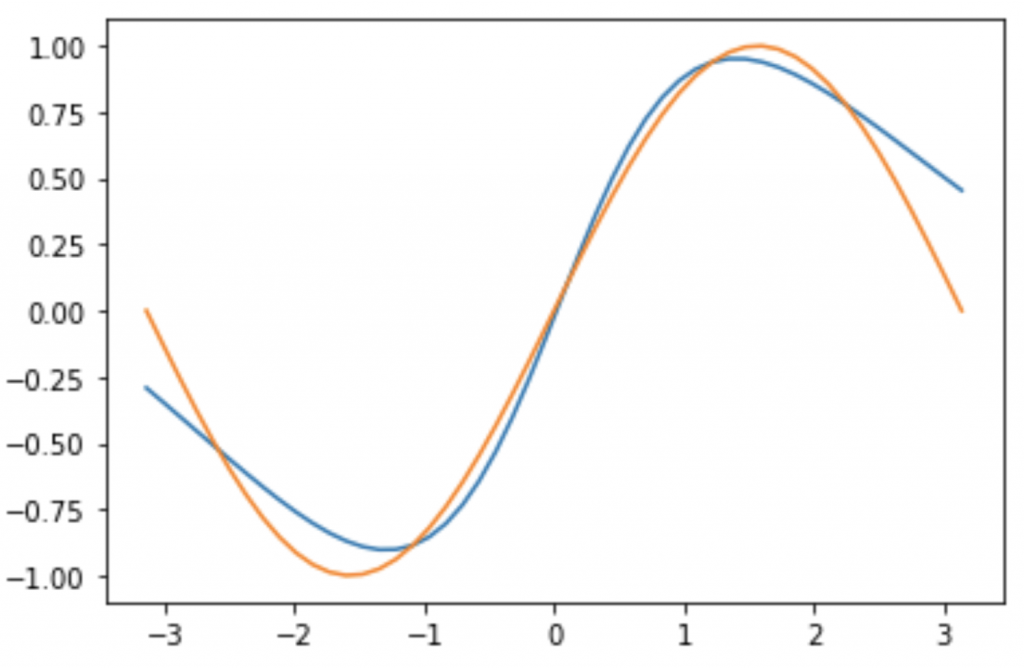
最後に
いかがだったでしょうか?
この記事を通して、少しでもあなたの困りごとが解決したら嬉しいです^^
📩 仕事の相談はこちら 📩
お仕事の相談のある方は、下記のフォームよりお気軽にご相談ください。
問い合わせフォームはこちら
もしもメールでの問い合わせの方がよろしければ、下記のメールアドレスへご連絡ください。
info*galirage.com(*を@に変えてご送付ください)
🎁 「生成AIの社内ガイドライン」PDFを『公式LINE』で配布中 🎁
「LINEで相談したい方」や「お問い合わせを検討中の方」は、公式LINEでご連絡いただけますと幸いです。
(期間限定で配信中なため、ご興味ある方は、今のうちに受け取りいただけたらと思います^^)
公式LINEはこちら
🚀 新サービス開始のお知らせ 🚀
新サービス 「AI Newsletter for Biz」 がスタートしました!
ビジネスパーソン向けに「AIニュース」を定期配信する完全無料のニュースレターです📩
ますみが代表を務める「株式会社Galirage」では、「生成AIを用いたシステムの受託開発(アドバイス活動含む)」をしています。
そこでお世話になっているお客様に対して、「最新トレンドを加味したベストな提案」をするために、日々最新ニュースを収集する仕組みを構築していました。
今回は、そこで構築した仕組みを活用して、より多くの人に有益な情報を届けたいと思い、本サービスを開始しました!
一人でも多くの方にとって、「AI人材としてのスキルアップ」につながれば幸いです^^
▼ 登録はこちらから ▼
https://bit.ly/ai_newsletter_for_biz_ai_lab